The method for balancing propellers that is most used in Rice Foundries is static balancing, since the propeller rotates on two parallel bars, which are fixed to the balancing bench and properly leveled with the ground where the benches are placed.

This technique consists of identifying the amount of weight and the position where material must be removed to compensate for the force exerted by the effect of the imbalance. This allows us to experience significant improvements in quality and performance, as it minimizes vibration in the propellers.

DEFINITION OF STATIC BALANCING

The most common definition of static balancing proposes using the net force, that is, an object is in static equilibrium when the sum of the forces acting on it (net or resultant force) is equal to zero. Both translational forces and torsional forces are considered and therefore an object is in static equilibrium if it is in translational equilibrium and in rotational equilibrium.

WHAT IS AN IMBALANCE?

Appears when the main axis of inertia is parallel to the axis of rotation.

They can have the same size and angular position and can be located at the same distance from the center of gravity of the rotor. If the rotor is resting on two level and thin supports, it will tend to rotate until the heavy point is at the bottom.

EFFECTS OF IMBALANCE

• Periodic vibrations of the equipment.
• Excessive wear.
• Bearing damage.
• Misadjustment in fixing systems.
• Transmitted vibrations.
• Increased energy consumption.
• Rotors friction in the housing body.
• Warming up.
• Increase in noise level during equipment operation.
• Damage to foundations of machinery and equipment.

STANDARD USED

All tolerances on marine propellers are governed by international standards. Rice uses the ISO 484 standard, which has different sections on how this verification should be carried out, the main variant being the propeller diameter. In one of the sections of said standard, it defines the maximum imbalance allowed.

For example, according to the standard for propellers greater than 2.50 meters in diameter, in section ISO 484/1, the maximum allowable balance weight (in kilograms) in the propeller TIP is defined by the following formulas:

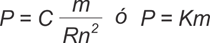
Where:
P = is the maximum allowable swing weight in kilograms.
m = is the weight of the propeller in kilograms.
R = is the radius of the propeller in meters.
n = are the revolutions per minute at which the propeller will rotate.
C and K = are constants that depend on the manufacturing class shown in the following table: